Types of Waves:

Transverse waves are waves with oscillating movement perpendicular to their direction of travel. Earthquake "shear" waves have this form. Light waves also have this form in that their electric and magnetic fields are perpendicular to the direction in which the light is propagating. In our class's lab you will induce transverse waves in springs by wiggling the springs side to side:

(Source: The Physics Classroom website - see link at the end of this page)

Longitudinal waves are waves with oscillations parallel to their direction of travel. Sound waves are longitudinal waves (with the wave moving in the same direction that the air is pushed and pulled). Similarly, in our class's lab you will induce longitudinal waves in springs by pushing and pulling on the ends of the springs:

(Source: The Physics Classroom website - see link at the end of this page)

Water Waves combine BOTH transverse and longitudinal motion with individual water molecules actually following almost circular paths (moving both side-to-side and front-to-back):

(Source: The Physics Classroom website - see link at the end of this page)

If this circular motion is hard to visualize, think of the underwater shots from surfing movies such as Blue Crush, or images such as these:

Source: Google images / paudie.worldpress,com	Source: Google images / bionomicfuel,com

Pulses appear to be single moving blips. But upon closer examination they can be explained as the "superposition" (sum) of waves having slightly different frequencies. In the weird field of "quantum mechanics" pulses can illustrate how a sum of waves can also behave like a particle (the famous "wave particle duality"):

Source: Wikepedia on waves. Their source: A. T. Fromhold (1991). "Wave packet solutions". Quantum Mechanics for Applied Physics and Engineering (Reprint of Academic Press 1981 ed.). Courier Dover Publications. pp. 59 ff. ISBN 0486667413. (p. 61)

Characteristics of Waves:

Amplitude is, loosely speaking, the intensity of a wave's oscillation. For a transverse wave, it is defined as the maximum deviation from a straight line (and not as the peak to valley shift which is then 2A):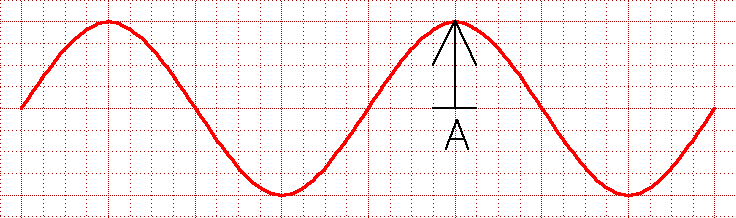

Wavelength is the distance over which a wave repeats. It can be measured peak to peak, or valley to valley. You might expect that it would be symbolized by W or L. Instead physicists use the Greek lower case lambda: λ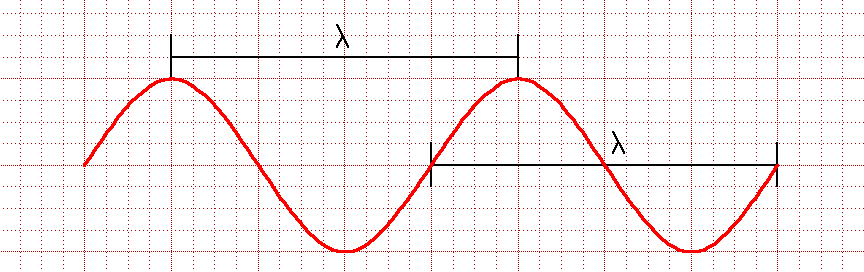

Phase is the part of a wave cycle that has passed an arbitrary point, or the offset between two waves. You might think that this would be measured in fractions of a wavelength. But because sine waves repeat every time their mathematical argument increases by 2π, phase is generally measured in terms of 2π. For instance, because these two waves are half of a wavelength out of sync, it is said that their phase differs by π: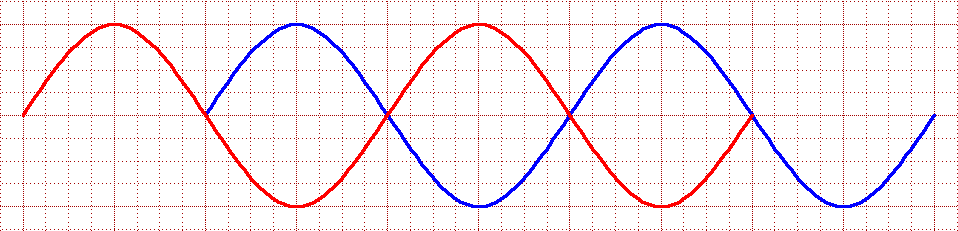

Period is the time it takes for the full cycle of a wave to pass a given point. Referring to that time, physicists use the capital letter T.

Frequency is how fast a wave oscillates. It used to be measured in "cycles per second" (or just 1/sec) but this has now been given the metric system name of a Hertz (capitalized because this was the name of a physicist). Electrical engineers use the letter f for frequency (but you will sometimes see physicists using the greek symbol nu: ν - sort of like a curved vee - to represent frequency measured in terms of 2π cycles per second).

A wave's period is the reciprocal of its frequency: T = 1 / f

Velocity of a wave can be deduced from its period and wavelength: In one period of a wave, it moves one wavelength. Thus:

A wave's velocity = λ / T = λ x f

Note: To help remember formulae, physicists often apply what they call dimensional analysis. As applied to this formula: Velocities have got to have units of distance / time, suggesting that the correct formula might be something that has length divided something that has time, or something with length multiplied by something with units of (1/time).

Interacting Waves

Reflected wave: The part of a wave that is returned by a boundary. A wave that completely returns (and doesn't propagate past that boundary) is said to be "100% reflected." As a wave reflects its phase can change depending on the type of boundary it encounters. In the lab you will test for such changes by either holding the ends of springs at a fixed point or tying them to a short length of string.

Refracted wave: The part of a wave that continues past a boundary. Depending on the nature of the boundary, the wave may change direction, amplitude, velocity and/or wavelength.

Superposition: The idea (also referred to as Huygen's Principle) that when two or more waves enter a certain region of space, the resulting pattern will be a simple sum of the individual waves. When the peaks of wave are in the same direction, and thus add to one another, this is referred to as constructive interference. When peaks of waves are in opposite directions, so that they tend to cancel one another, this is referred to as destructive interference.

Standing wave: A wave that that seems remain in one position (i.e. with zero velocity), simply oscillating back and forth. Standing waves are created when a wave is confined to a box whose length is a multiple of the wave's wavelength / 2. This condition means that when the peak of a moving wave starts at one end of the box, travels its length, reflects, and returns back to its starting point, it will then have traveled a multiple of that wave's wavelength. The original wave and its reflection will then "superimpose" to "constructively interfere." Standing waves are all around you but the most familiar may be the 2D circular standing waves on the surface of your cup of coffee:

Source: Wikepedia on waves.

Node: On a standing wave (or a given portion of a moving wave), the points that move the least (i.e. the “zero-crossings” of the wave).

Anti-node: On a standing wave (or a given portion of a moving wave), the points that move the most.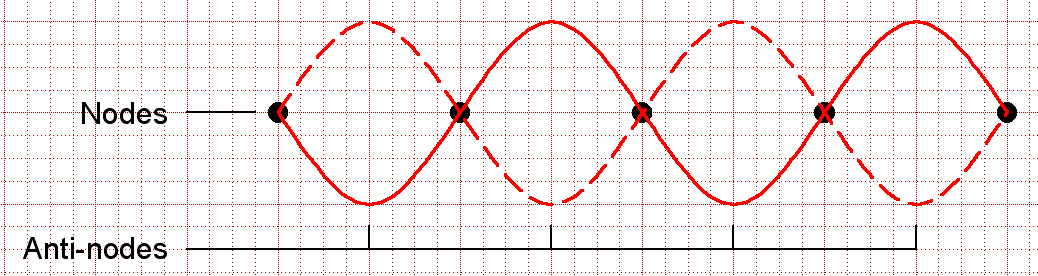

To learn more:

This review drew from:

The Physics Classroom website, Waves - lesson 1:

http://www.physicsclassroom.com/class/waves/u10l1c.cfm

Wikipedia's page on waves:

http://en.wikipedia.org/wiki/Wave

For more detailed information, and illustrations, please visit those websites

Copyright: John C. Bean